


STANDING WAVES
WHAT ARE THEY?
WAVES IN THE REAL WORLD
In the open ocean, normal water waves continue to travel (until they run out of energy) but when they go from deep water to a steep shore line quickly, they will be reflected back just like the voltage waves at the end of an antenna. If the wave front is parallel to he cliff, standing waves develop. A boat can be anchored away from a cliff at a quarter of the wavelength of a big swell with perfect safety. The same for 3/4 of a wavelength and so forth. At these points the boat rocks a little from side to side but doesn't go up and down much. This is a perfect standing wave and the point where the boat is anchored is called a node.
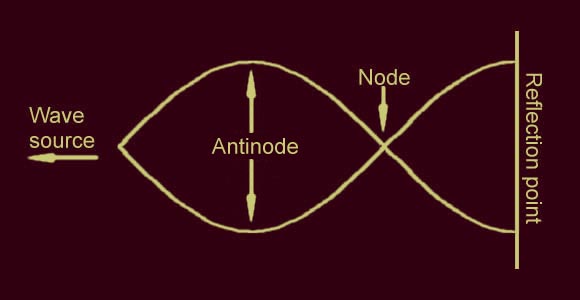
Suppose now we place another reflection point a quarter of a wavelength away in the opposite direction. Also suppose now we push the water (or whatever medium we are looking at) back and forth at the resonant frequency, standing waves will develop. Movement up and down at the reflection points will be a lot more than at the node. For water waves this frequency will be dependant on the depth, density etc. of the water.

You can try this for yourself with a tray of water. If you place a couple of corks in the water and rock the tray back and forth, you can see which ones go up and down. If this doesn't look like the voltage distribution along a half wave dipole then you are blind or not looking. Electrically, an SWR meter is designed to measure how far away from the cliff we are pushing back and forth. In an antenna, we are talking about voltage waves and not water but the physics and priciples are exactly the same.
TAKE SPECIAL NOTE
1) THIS APPLIES TO THE ANTENNA NOT THE TRANSMISSION LINE. Standing waves are NOT things that travel around the place along wires. If the antenna is resonant (has a pefect standing wave because that's the definition of resonance) it will appear as if it is a resistor. A resistor is a passive component and doesn't reflect waves so there will be no standing waves apparent in the feeder.
2) WITH AN SWR meter, WE ARE NOT TRYING TO MEASURE "STANDING WAVES" - WE ARE TRYING TO MEASURE STANDING WAVE RATIO.
WHAT HAPPENS IF WE PUSH THE WAVES AT OTHER THAN THE RESONANT FREQUENCY
The diagrams below show what happens if we drive waves at a frequency other than the resonant one. The first diagram shows what happens if the reflection point (end of antenna) is too close. At the node, voltage develops and reflected power must be absorbed by the output transistors. When the reflection point is too far away (second diagram), the transistors are pushing before the reflected wave gets there and are pushing for nothing and again must absorb the energy. Energy being absorbed by the transistors isn't being radiated and only serves to cook the amplifier.
This is the case when the relection point is too close. RF waves are reflected because the current has nowhere to go. The current is on its way back before the full voltage reaches the end. The current leads the voltage so the reflection point appears as a capacitance. |
This is the case when the reflection point is too far away. The current is still building up while the voltage has already started to decline. The current lags the voltage so it appears as an indutance. |
In actuallity this isn't quite the explaination but it was the best I could do.
The transistors can only produce so much power safely. They can be either overdriven or overheated by a bad Standing Wave Ratio in either direction ie. too long (inductive) or too short (capacitive).
Calculating the SWR is complex. It involves imaginary numbers but the absolute value turns out to be:-
SW Ratio = (1 + Vr / Vf ) / ( 1 - Vr / Vf ) : 1
OR
SW Ratio = (1 + √ ( Pr / Pf) ) / ( 1 - √ (Pr / Pf) ) : 1
For most amateur purposes this is enough but there is a good article in wikipedia if you want to know more.
For a perfect standing wave:-
Vr = 0 and so Vr / Vf = zero resulting in a SWR value of (1+0)/(1-0) : 1 or 1 : 1
(NOTE - this is a RATIO not the numerical value of 1.1).
For the worst case scenario when Vr = Vf (There can't be more reflected than sent):-
Vr / Vf = 1 so, for the bottom of the equation, 1 - Vr / Vf = 0
dividing by zero yields an infinite SWR ratio value.

All text and images on this site are Copyright to John Langsford (vk5ajl).
You may provide links on other sites or use the information and pictures for your own personal use.
You may use the text or images for redisplay or quotation provided you acknowledge the source ie. vk5ajl.com.
I think that's pretty fair, don't you?